1. 项目准备

1.1. 问题导入

图像分类是根据图像的语义信息将不同类别图像区分开来，是计算机视觉中重要的基本问题。现有10类若干张手写数字图片，请训练多层感知机（MLP）模型预测手写数字图片：

1.2. 数据集简介

本实验使用的是PaddlePaddle提供的mnist数据集（paddle.dataset.mnist），它包含60000个训练集和10000测试数据集，分为图片和标签，图片是 28 * 28 的像素矩阵，标签为0~9共10个数字：

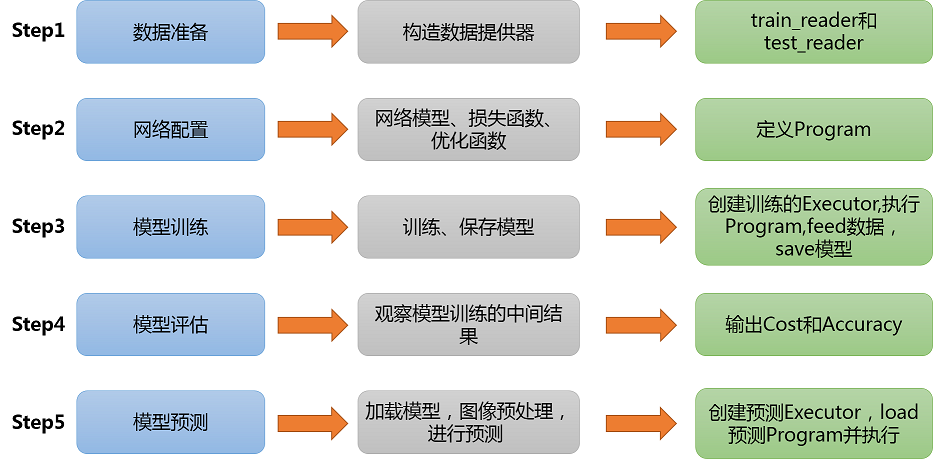
2. 实验步骤

2.0. 前期准备

导入模块

注意：本案例仅适用于PaddlePaddle 2.0+版本

import numpy as np
from PIL import Image
from random import randint
from matplotlib import pyplot as plt

import paddle
from paddle import nn
from paddle import metric as M
from paddle.io import DataLoader
from paddle.nn import functional as F
from paddle.optimizer import Adam
from paddle.vision.datasets import MNIST
from paddle.vision.transforms import Compose, Normalize

设置超参数

BATCH_SIZE = 128                # 每批次的样本数
CLASS_DIM = 10                  # 图像种类数
EPOCHS = 4                      # 训练轮数
LOG_GAP = 200                   # 输出训练信息的间隔
INIT_LR = 2e-4                  # 初始学习率
DATA_PATH = "./data"            # 数据集存放路径
MODEL_PATH = "MLP.pdparams"     # 模型参数保存路径

2.1. 数据准备

数据预处理

transform = Compose([
    Normalize(mean=[127.5], std=[127.5], data_format='CHW')  # 归一化
])
train_dataset = MNIST(mode='train', transform=transform)     # 训练集
test_dataset = MNIST(mode='test', transform=transform)       # 测试集

定义数据读取器

batch_size：每批次读取样本数。例如batch_size=64表示每批次读取64个样本。

shuffle：是否打乱样本。例如shuffle=True表示在取数据时打乱样本顺序，以减少过拟合发生的可能。

drop_last：是否丢弃不完整的批次样本。例如drop_last=True表示丢弃因数据集样本数不能被batch_size整除而产生的最后一个不完整的batch样本。

num_workers：加载数据的子进程个数。num_workers的值设为大于0时，即开启多进程方式异步加载数据，可提升数据读取速度。

train_loader = DataLoader(train_dataset,          # 训练数据集
                          batch_size=BATCH_SIZE,  # 每批读取的样本数
                          num_workers=1,          # 加载数据的子进程个数
                          shuffle=True,           # 打乱训练数据集
                          drop_last=True)         # 丢弃不完整的样本

test_loader = DataLoader(test_dataset,            # 测试数据集
                         batch_size=BATCH_SIZE,   # 每批读取的样本数
                         num_workers=1,           # 加载数据的子进程个数
                         shuffle=False,           # 不打乱测试数据集
                         drop_last=True)          # 丢弃不完整的样本

2.2. 模型配置

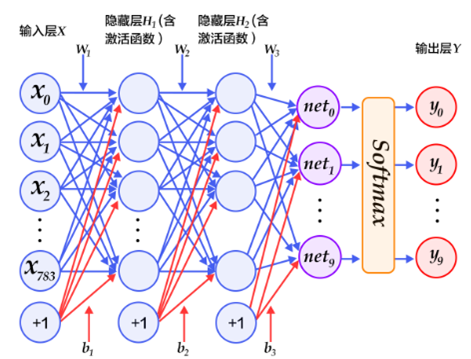
定义多层感知机
本实验定义的是一个多层感知机，它一共有三层（不含输入层）：即两个大小为512的隐藏层和一个大小为10的输出层。

class MLP(nn.Layer):
    ''' Multi-Layer Perceptron (MLP) '''

    def __init__(self, n_classes=10):
        super(MLP, self).__init__()
        self.model = nn.Sequential(
            nn.Flatten(1, -1),
            nn.Linear(28*28, 1024),     # 第一个全连接隐藏层
            nn.ReLU(),
            nn.Dropout(0.25),
            nn.Linear(1024, n_classes)  # 第二个全连接隐藏层
        )

    def forward(self, x):
        return self.model(x)

模型实例化

1	model = MLP(n_classes=CLASS_DIM)

2.3. 模型训练

model.train()                # 开启训练模式
opt = Adam(learning_rate=INIT_LR,
           parameters=model.parameters())  # 定义Adam优化器
loss_arr, acc_arr = [], []   # 用于可视化

for ep in range(EPOCHS):
    for batch_id, data in enumerate(train_loader()):
        x_data, y_data = data
        y_pred = model(x_data)                  # 预测结果
        acc = M.accuracy(y_pred, y_data)        # 计算准确率
        loss = F.cross_entropy(y_pred, y_data)  # 计算交叉熵
        if batch_id % LOG_GAP == 0:             # 定期输出训练结果
            print("Epoch：%d，Batch：%3d，Loss：%.5f，Acc：%.5f"\
                % (ep, batch_id, loss, acc))
        acc_arr.append(acc.item())
        loss_arr.append(loss.item())
        opt.clear_grad()
        loss.backward()
        opt.step()

paddle.save(model.state_dict(), MODEL_PATH)  # 保存训练好的模型

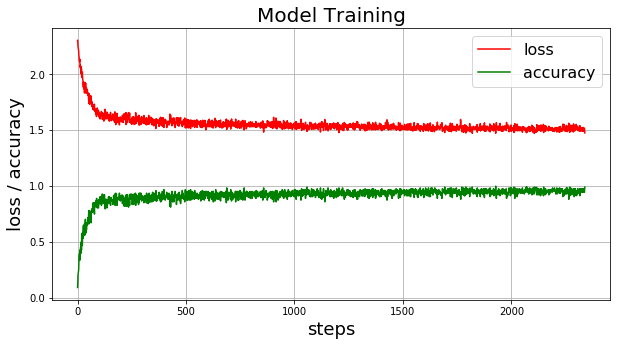
模型训练的结果如下：

Epoch：0，Batch：  0，Loss：2.63496，Acc：0.14062
Epoch：0，Batch：200，Loss：0.42945，Acc：0.86719
Epoch：0，Batch：400，Loss：0.19543，Acc：0.96094
Epoch：1，Batch：  0，Loss：0.18954，Acc：0.96094
Epoch：1，Batch：200，Loss：0.18587，Acc：0.95312
Epoch：1，Batch：400，Loss：0.18084，Acc：0.96094
Epoch：2，Batch：  0，Loss：0.12029，Acc：0.97656
Epoch：2，Batch：200，Loss：0.18207，Acc：0.95312
Epoch：2，Batch：400，Loss：0.18604，Acc：0.92188
Epoch：3，Batch：  0，Loss：0.14635，Acc：0.97656
Epoch：3，Batch：200，Loss：0.13389，Acc：0.95312
Epoch：3，Batch：400，Loss：0.06493，Acc：0.99219

可视化训练过程

plt.figure(figsize=[10, 5])
plt.title("Model Training", fontsize=20)
plt.xlabel("steps", fontsize=18)
plt.ylabel("loss / accuracy", fontsize=18)
plt.plot(range(len(loss_arr)), loss_arr, color="r", label="loss")
plt.plot(range(len(acc_arr)), acc_arr, color="g", label="accuracy")
plt.legend(fontsize=16)
plt.grid()
plt.show()

2.4. 模型评估

model.eval()                 # 开启评估模式
test_costs, test_accs = [], []

for batch_id, data in enumerate(test_loader()):
    x_data, y_data = data
    y_pred = model(x_data)                  # 预测结果
    acc = M.accuracy(y_pred, y_data)        # 计算准确率
    loss = F.cross_entropy(y_pred, y_data)  # 计算交叉熵
    test_accs.append(acc.item())
    test_costs.append(loss.item())
test_loss = np.mean(test_costs)    # 每轮测试的平均误差
test_acc = np.mean(test_accs)      # 每轮测试的平均准确率
print("Eval \t Loss：%.5f，Acc：%.5f" % (test_loss, test_acc))

模型评估的结果如下：

1	Eval Loss：0.09750，Acc：0.97296

2.5. 模型预测

准备预测数据

这是预测数据集的下载链接：手写数字预测数据集 - AI Studio，它包含从0到9的10张数字图片。

def load_image(path):        # 图片预处理
    # (1) 打开并展示图像：
    img = Image.open(path)   # 打开图像
    plt.imshow(img)
    plt.show()               # 显示图像

    # (2) 格式化图像：
    img = img.convert("L")                 # 将图像转化为灰度图像，L代表灰度图像
    img = img.resize((28, 28), Image.ANTIALIAS)  # 将图像缩放为28*28的高质量图像
    img = np.array(img).reshape(1, 1, 28, 28)\
        .astype(np.float32)          # 把图像变成一个numpy数组以匹配数据馈送格式
    img = img / 255.0 * 2.0 - 1.0    # 将数据归一化到[-1, 1]之间
    img = paddle.to_tensor(img)      # 将图像转化为Tensor类型
    return img


truth_lab = randint(0, 9)                     # 预测图片的真实标签
img_path = DATA_PATH + "/infer_%d.png"        # 预测图片的路径
infer_img = load_image(img_path % truth_lab)  # 获取预测图片

随机选取的预测图片如下：

载入模型并开始预测

model.eval()                    # 开启评估模式
model.set_state_dict(
    paddle.load(MODEL_PATH)
)   # 载入预训练模型参数
result = model(infer_img)
infer_lab = np.argmax(result)   # 返回数组result中的最大值的索引值
print("真实标签：%d，预测结果：%d" % (truth_lab, infer_lab))

模型预测的结果如下：

1	真实标签：2，预测结果：2

写在最后

如果您发现项目存在问题，或者如果您有更好的建议，欢迎在下方评论区中留言讨论~

这是本项目的链接：实验项目 - AI Studio，点击fork可直接在AI Studio运行~

这是我的个人主页：个人主页 - AI Studio，来AI Studio互粉吧，等你哦~