1. 项目准备

1.1. 问题导入

KMeans聚类算法是一种非层次聚类算法，在最小误差的基础上将数据划分了特定的类，类间利用距离作为相似度指标，两个向量之间的距离越小，其相似度就越高。已知中国部分二级城市的经纬度，要求利用经纬度坐标进行KMeans聚类分析。

1.2. 数据集简介

本案例的数据集包含4列351行数据，每行数据包含一个城市，其中前两列为城市所在省和市，最后两列为城市的经纬度。

这是数据集的下载链接：中国主要城市经纬度数据集 - AI Studio

2. K-Means算法

2.1. 算法特点

K-Means聚类算法是一种基于向量距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。该算法认为类簇是由距离靠近的对象组成的，因此它把得到紧凑且独立的类簇作为聚类的最终目标。
综上所述，K-Means算法划分的k个聚类具有以下特点：各聚类内部的元素尽可能的紧凑，而各聚类之间的元素尽可能的分开。

2.2. 算法流程

K-Means算法的基础是最小误差平方和准则，K-Means算法具体流程如下：
（1）从n个样本对象任意选择k个对象作为初始聚类中心；
（2）根据在步骤 (1) 中设置的k个聚类中心，计算每个对象与这k个中心的距离；
（3）经过步骤 (2) 的计算，所有对象与这个k个中心的距离就计算出来了，接着把所有对象与离它最近的中心归在一个类簇中；
（4）重新计算每个类簇的中心对象的位置；
（5）重复步骤 (3) 和 (4)，直到类簇聚类方案中的对象归类几乎不发生变化为止。

2.3. 算法缺陷

（1）种子点的个数要事先确定，但是我们一般很难估计它的个数。
（2）K-Means算法需要初始种子点，并且随机种子会影响计算结果。
（3）需要不断地计算调整后的类簇中心，当数据量很大时，这个计算所需的时间就会很大。

2.4. 算法改进

K-Means++算法是改进后的K-Means算法，具体算法流程如下：
（1）从数据集的点中随机选择一个点作为种子点；
（2）计算数据集中的每一个点到种子点的距离D(x)；
（3）选择D(x)较大的点作为新的种子点；
（4）重复步骤 (2) 和 (3)直到新的种子被选出来。

3. 实验步骤

3.1. 前期准备

  • 导入模块
1
2
3
4
5
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score, silhouette_samples
  • 设置超参数
1
2
3
4
N_CLUSTERS = 7                                     # 类簇的数量
MARKERS = ['*', 'v', '+', '^', 's', 'x', 'o']      # 标记样式（绘图）
COLORS = ['r', 'g', 'm', 'c', 'y', 'b', 'orange']  # 标记颜色（绘图）
DATA_PATH = './data/China_cities.csv'              # 数据集路径

3.2. 读入数据

1
2
df = pd.read_csv(DATA_PATH)
print(df.head())    # 展示前5行数据

前5行数据的输出结果：

1
2
3
4
5
6
     省级行政区      城市       北纬        东经
0       北京        北京市   39.904690   116.40717
1       天津        天津市   39.085100   117.19937
2       上海        上海市   31.230370   121.47370
3       重庆        重庆市   29.564710   106.55073
4  香港特别行政区    九龙    22.327115   114.17495

3.3. 数据预处理

我们需要将各城市的经纬度数据单独提取出来。

1
2
3
x = df.drop('省级行政区', axis=1)
x = x.drop("城市", axis=1)
x_np = np.array(x)        # 将x转化为numpy数组

3.4. 模型构建与训练

本项目使用K-Means聚类算法来对城市的经纬度特征进行聚类。

1
2
model = KMeans(N_CLUSTERS)      # 构建聚类器
model.fit(x)                    # 训练聚类器
  • 计算轮廓系数
    轮廓系数（Silhouette Coefficient）是一种评价聚类效果的方法，其值介于[−1,1][-1, 1]之间，值越趋近于11代表同簇点的内聚度和异簇点的分离度都相对较优。
    假设我们用K-Means算法将数据划分成KK个类簇，对于某簇中任意一个向量ii而言，其轮廓系数Si=Bi−Aimax(Ai,Bi)S_i = \frac{B_i-A_i}{max(A_i, B_i)}。其中，AiA_i是ii到同簇中其它所有点距离的平均值，它是ii与同簇内其他点不相似程度的平均值；BiB_i是ii到其他簇内所有点平均距离的最小值，它是ii与其他簇的点平均不相似程度的最小值。
    将所有点的轮廓系数求平均，就能得到该聚类结果总的轮廓系数。
1
2
3
4
labels = model.labels_      # 获取聚类标签

# print(silhouette_samples(x, labels))  # 获取所有样本的轮廓系数
print(silhouette_score(x, labels))      # 获取聚类结果总的轮廓系数

模型的轮廓系数如下：

1
0.40034267246878397

3.5. 导出类簇信息

  • 导出类簇中心
1
print(model.cluster_centers_)	# 输出类簇中心

最终的类簇中心如下：

1
2
3
4
5
6
7
[[ 36.30742841 105.21526409]
 [ 27.85671809 102.12971362]
 [ 41.34384438  84.09634   ]
 [ 44.01411423 124.90852352]
 [ 24.3572954  111.87362376]
 [ 29.06106948 118.51486687]
 [ 36.22217001 115.34626425]]
  • 导出类簇元素
1
2
3
for i in range(N_CLUSTERS):
    print(f" CLUSTER-{i+1} ".center(60, '='))
    print(df[labels == i])

各类簇包含的元素如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
======================== CLUSTER-1 =========================
    省级行政区   城市         北纬          东经
2      上海  上海市  31.230370  121.473700
10    台湾省  台中市  24.138620  120.679510
11    台湾省  台北市  25.037798  121.565170
..    ...  ...        ...         ...
======================== CLUSTER-2 =========================
     省级行政区           城市        北纬         东经
3       重庆          重庆市  29.56471  106.55073
221    四川省          成都市  30.57020  104.06476
222    四川省          自贡市  29.33920  104.77844
..    ...  ...        ...         ...
======================== CLUSTER-3 =========================
      省级行政区     城市        北纬         东经
0        北京    北京市  39.90469  116.40717
1        天津    天津市  39.08510  117.19937
17      河北省   石家庄市  38.04276  114.51430
..      ...    ...       ...        ...
======================== CLUSTER-4 =========================
        省级行政区           城市        北纬        东经
336     西藏自治区         阿里地区  30.40051  81.14540
337  新疆维吾尔自治区        乌鲁木齐市  43.82663  87.61688
338  新疆维吾尔自治区        克拉玛依市  45.57999  84.88927
..      ...    ...       ...        ...
======================== CLUSTER-5 =========================
       省级行政区    城市         北纬          东经
4    香港特别行政区    九龙  22.327115  114.174950
5    香港特别行政区    新界  22.341766  114.202408
6    香港特别行政区   香港岛  22.266416  114.177314
..       ...   ...        ...         ...
======================== CLUSTER-6 =========================
      省级行政区        城市         北纬          东经
73      辽宁省       沈阳市  41.677180  123.463100
74      辽宁省       大连市  38.913690  121.614760
75      辽宁省       鞍山市  41.107770  122.994600
..       ...   ...        ...         ...
======================== CLUSTER-7 =========================
       省级行政区          城市        北纬         东经
267      陕西省         西安市  34.34127  108.93984
268      陕西省         铜川市  34.89673  108.94515
269      陕西省         宝鸡市  34.36194  107.23732
..       ...   ...        ...         ...

3.6. 类簇可视化

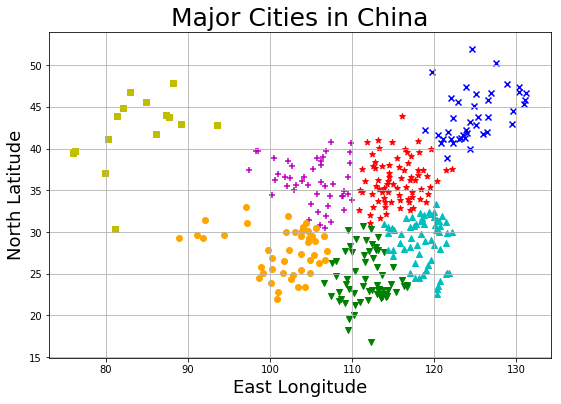
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
plt.figure(figsize=(9, 6))
plt.title("Major Cities in China", fontsize=22)
plt.xlabel('East Longitude', fontsize=18)
plt.ylabel('North Latitude', fontsize=18)

for i in range(N_CLUSTERS):
    members = labels == i      # members是一个布尔型数组
    plt.scatter(
        x_np[members, 1],      # 城市经度数组
        x_np[members, 0],      # 城市纬度数组
        marker = MARKERS[i],   # 标记样式
        c = COLORS[i]          # 标记颜色
    )   # 绘制散点图

plt.grid()
plt.show()

基于经纬度的城市聚类结果：
Results

写在最后

  • 如果您发现项目存在问题，或者如果您有更好的建议，欢迎在下方评论区中留言讨论~
  • 这是本项目的链接：实验项目 - AI Studio，点击fork可直接在AI Studio运行~
  • 这是我的个人主页：个人主页 - AI Studio，来AI Studio互粉吧，等你哦~