1. 项目准备

1.1. 问题导入

构建一个模型，根据鸢尾花的花萼大小和花瓣大小将其分为三种不同的品种：

1.2. 数据集简介

数据集共包含150行数据，每一行数据由四个特征值及一个目标值组成。
其中，四个特征值分别为：萼片长度、萼片宽度、花瓣长度、花瓣宽度；
目标值是鸢尾花的类别，即：Iris Setosa、Iris Versicolour、Iris Virginica。

这是数据集的下载链接：鸢尾花数据集 - AI Studio

2. 实验步骤

2.0.导入模块

1
2
3
4
5
import numpy as np
from sklearn import svm
from sklearn.model_selection import train_test_split
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt

2.1. 数据准备

  • 数据编码
1
2
3
4
5
6
7
def iris_type(s):   # 将鸢尾花的种类以整数形式表示，便于数据加载
    it = {
        b'Iris-setosa': 0,      # 山鸢尾
        b'Iris-versicolor': 1,  # 变色鸢尾
        b'Iris-virginica': 2    # 维吉尼亚鸢尾
    }
    return it[s]
1
2
3
4
5
6
7
data_path = 'iris.data'
data = np.loadtxt(
    data_path,                  # 数据文件的路径
    dtype=float,                # 数据类型
    delimiter=',',              # 数据分隔符
    converters={4: iris_type}   # 将第5列数据用iris_type进行转换
)   # data为二维数组，且data.shape=(150, 5)
  • 数据分割
1
2
3
4
5
6
x, y = np.split(
    data,       # 要切分的数组
    (4, ),      # 沿轴切分的位置，前4列为x，第5列开始往后为y
    axis=1      # 1代表纵向按列分割；默认0代表横向按行分割
)
x = x[:, 0:2]   # 为方便后期画图更直观，我们取x中的前两列作为特征
  • 数据集划分
1
2
3
4
5
6
x_train, x_test, y_train, y_test = train_test_split(
    x,                # 要划分的样本特征集
    y,                # 要划分的样本结果集
    random_state=1,   # 随机数种子
    test_size=0.3     # 测试样本占比
)

2.2. 模型搭建

  • 惩罚系数 C
  • C值大，对误分类的惩罚增大，这样趋向于训练集测试的准确率很高，但泛化能力弱
  • C值小，对误分类的惩罚减小，允许容错，泛化能力较强
  • 内核 kernel
  • “linear”代表“线性核”，“rbf”代表“高斯核”。
  • 高斯核函数参数 gamma *
  • gamma是选择rbf函数作为kernel后，该函数的一个参数，它隐含地决定了数据映射到新的特征空间后的分布。
  • gamma越小，分类界面越连续；gamma越大，分类界面越“散”，分类效果越好，但可能过拟合。
  • 划分方法 decision_function_shape
  • “ovr”代表“one v rest”，即一个类别与其他类别进行划分；
  • “ovo”代表“one v one”，即将类别两两之间进行划分，用二分类的方法模拟多分类的结果。
1
2
3
4
# 高斯核的svm分类器：
# clf = svm.SVC(C=0.8, kernel='rbf', gamma=50, decision_function_shape='ovr')
# 线性核的svm分类器：
clf = svm.SVC(C=0.5, kernel='linear', decision_function_shape='ovr')

2.3. 模型训练

1
2
3
clf.fit(x_train,            # 训练集特征向量
        y_train.ravel())    # 训练集目标值；ravel()函数可将矩阵转变成一维数组

2.4. 模型评估

  • 评分与准确率
1
2
3
def show_accuracy(a, b, tip):   # 判断a和b是否相等，并计算准确率的均值
    acc = a.ravel() == b.ravel()
    print("%s上的准确率 \t %.3f" % (tip, np.mean(acc)))
1
2
3
4
5
print("训练集上的评分 \t %.3f" % clf.score(x_train, y_train))
print("测试集上的评分 \t %.3f" % clf.score(x_test, y_test))

show_accuracy(clf.predict(x_train), y_train, "训练集")
show_accuracy(clf.predict(x_test), y_test, "测试集")
1
2
3
4
训练集上的评分 	 0.819
测试集上的评分 	 0.778
训练集上的准确率 	 0.819
测试集上的准确率 	 0.778
  • 决策函数的值
    决策函数的值表示x到各分割平面的距离。
1
2
3
4
values = clf.decision_function(x_train)
print("Iris-setosa \t Iris-versicolor \t Iris-virginica")
for lt in values:
    print("%9.6f \t %9.6f \t\t %9.6f" % tuple(lt))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
Iris-setosa 	 Iris-versicolor 	 Iris-virginica
-0.500000 	  1.208873 		  2.291127
 2.063288 	 -0.076968 		  1.013680
 2.166750 	  0.917028 		 -0.083778
 2.114278 	  0.997652 		 -0.111931
 0.992554 	  2.063921 		 -0.056475
 2.117430 	  0.952555 		 -0.069985
 2.056150 	 -0.041847 		  0.985697
-0.318666 	  1.026860 		  2.291806
-0.271663 	  1.091503 		  2.180159
-0.378276 	  1.142604 		  2.235671
-0.221507 	  1.111050 		  2.110458
-0.183312 	  2.100667 		  1.082645
-0.054450 	  0.999278 		  2.055172
-0.469778 	  1.178538 		  2.291240
-0.057601 	  2.044375 		  1.013226
 2.174723 	  0.936981 		 -0.111704
-0.133157 	  2.120214 		  1.012943
-0.217521 	  2.121026 		  1.096495
 2.114278 	  0.997652 		 -0.111931
 2.163598 	  0.962125 		 -0.125724
-0.210383 	  1.085906 		  2.124477
 2.212918 	  0.926599 		 -0.139517
-0.133992 	  1.065140 		  2.068852
-0.180161 	  1.055570 		  2.124590
-0.233467 	  1.081121 		  2.152346
-0.087824 	  2.074710 		  1.013113
-0.203245 	  1.050785 		  2.152460
-0.114894 	  1.059949 		  2.054945
 2.177874 	 -0.108116 		  0.930242
-0.235784 	  2.181291 		  1.054492
-0.206396 	  1.095882 		  2.110514
-0.210383 	  1.085906 		  2.124477
-0.029695 	  2.114210 		  0.915486
-0.126854 	  1.030020 		  2.096834
-0.094962 	  2.109831 		  0.985131
 2.105470 	 -0.077374 		  0.971904
 2.110292 	  0.987676 		 -0.097968
 2.204110 	 -0.148428 		  0.944318
-0.203245 	  1.050785 		  2.152460
 2.190669 	  0.976887 		 -0.167556
-0.160228 	  2.105452 		  1.054776
-0.236619 	  1.126218 		  2.110401
-0.095797 	  2.054758 		  1.041039
 2.113443 	 -0.057421 		  0.943978
 2.102319 	  0.967723 		 -0.070042
-0.122032 	  2.095070 		  1.026963
 2.110292 	  0.987676 		 -0.097968
-0.412485 	  1.162964 		  2.249521
-0.168201 	  1.085499 		  2.082701
-0.420458 	  1.143011 		  2.277447
-0.248578 	  1.096288 		  2.152290
-0.277966 	  2.181698 		  1.096268
-0.092645 	  1.009660 		  2.082985
-0.253400 	  1.031238 		  2.222161
-0.053615 	  2.054351 		  0.999263
 2.153955 	 -0.167975 		  1.014019
-0.122032 	  2.095070 		  1.026963
 2.065793 	  1.088253 		 -0.154046
-0.110073 	  2.124999 		  0.985074
-0.271663 	  1.091503 		  2.180159
 2.136527 	  0.947364 		 -0.083891
-0.297898 	  1.131815 		  2.166083
 2.151639 	  0.932196 		 -0.083835
 2.174723 	  0.936981 		 -0.111704
-0.111743 	  1.014852 		  2.096891
-0.068726 	  2.069519 		  0.999207
-0.237454 	  1.071144 		  2.166309
 2.121416 	  0.962532 		 -0.083948
 2.162763 	 -0.092948 		  0.930185
-0.065574 	  1.024422 		  2.041152
 2.167585 	  0.972102 		 -0.139687
-0.122032 	  2.095070 		  1.026963
 2.129389 	  0.982485 		 -0.111874
-0.210383 	  1.085906 		  2.124477
 2.019625 	  1.078683 		 -0.098307
 2.182696 	  0.956934 		 -0.139630
-0.161063 	  1.050379 		  2.110684
 2.209767 	  0.971696 		 -0.181462
-0.038504 	  2.039183 		  0.999320
 2.175558 	  0.992055 		 -0.167613
-0.110073 	  2.124999 		  0.985074
-0.075029 	  2.159713 		  0.915316
 2.132541 	  0.937388 		 -0.069928
 2.095180 	  1.002844 		 -0.098024
 1.004513 	  2.093851 		 -0.098364
 2.243141 	  0.896263 		 -0.139403
-0.095797 	  2.054758 		  1.041039
-0.149103 	  1.080308 		  2.068795
 2.136527 	  0.947364 		 -0.083891
-0.233467 	  1.081121 		  2.152346
-0.072712 	  2.059543 		  1.013170
-0.273979 	  2.191674 		  1.082305
-0.275649 	  1.081527 		  2.194122
-0.122032 	  2.095070 		  1.026963
 2.060137 	 -0.031871 		  0.971734
 2.076083 	  1.008035 		 -0.084118
-0.194437 	  2.125811 		  1.068625
-0.164214 	  2.095476 		  1.068739
-0.344067 	  1.122245 		  2.221822
-0.118046 	  2.105046 		  1.013000
-0.202410 	  1.105859 		  2.096551
-0.176174 	  1.065547 		  2.110627
-0.247743 	  2.151362 		  1.096381
-0.233467 	  1.081121 		  2.152346
 2.110292 	  0.987676 		 -0.097968

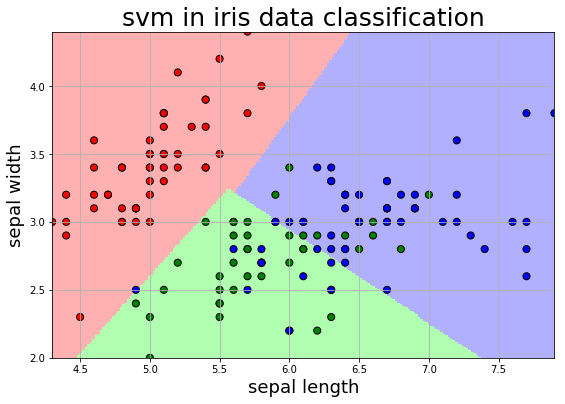
2.5. 可视化展示

1
2
3
4
5
6
7
x1_min, x1_max = x[:, 0].min(), x[:, 0].max()   # 第0列的最小值和最大值
x2_min, x2_max = x[:, 1].min(), x[:, 1].max()   # 第1列的最小值和最大值
x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j]   # 生成网格采样点

grid_test = np.stack((x1.flat, x2.flat), axis=1)    # 分别在第0维和第2维加入数组
z = clf.decision_function(grid_test)                # 样本到决策面的距离
grid_hat = clf.predict(grid_test)                   # 预测鸢尾花类别，得到分类值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
plt.figure(figsize=[9, 6])
plt.title("svm in iris data classification", fontsize=25)
tags = ['sepal length', 'sepal width', 'petal length', 'petal width']   # 特征标签
plt.xlabel(tags[0], fontsize=18)
plt.ylabel(tags[1], fontsize=18)
plt.xlim(x1_min, x1_max)      # x轴的上下限
plt.ylim(x2_min, x2_max)      # y轴的上下限

# 绘制背景：
cm_light = ListedColormap(['#FFB0B0', '#B0FFB0', '#B0B0FF'])   # 背景颜色
grid_hat = grid_hat.reshape(x1.shape)         # 使得grid_hat和x1的形状一致
plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light)

# 绘制样本点和测试点：
cm_dark = ListedColormap(['red', 'green', 'blue'])   # 数据点颜色
plt.scatter(x[:, 0], x[:, 1], c=np.squeeze(y), edgecolor='k', s=50, cmap=cm_dark)
plt.scatter(x_test[:, 0], x_test[:, 1], s=120, facecolor="none", zorder=10)

plt.grid()
plt.show()

写在最后

  • 如果您发现项目存在问题，或者如果您有更好的建议，欢迎在下方评论区中留言讨论~
  • 这是本项目的链接：实验项目 - AI Studio，点击fork可直接在AI Studio运行~
  • 这是我的个人主页：个人主页 - AI Studio，来AI Studio互粉吧，等你哦~