1. 项目准备
1.1. 回归问题
回归模型可以理解为:存在一个点集,用一条曲线去拟合它分布的过程。
1.2. 问题导入
请根据以往在每件商品的广告费用和实际销量,预测未来商品的销量。
1.3. 数据集简介
数据共4列200行,每一行为一个特定的商品,前3列为输入特征,最后一列为输出特征。
输入特征 输出特征
这是数据集的下载链接:商品广告费与销量数据集 - AI Studio
2. 实验步骤
2.0.导入模块
1 2 3 4 5 6 import pandas as pdimport numpy as npfrom sklearn import metricsfrom sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LinearRegressionimport matplotlib.pyplot as plt
2.1. 数据获取
1 2 3 df = pd.read_csv("Advertising.csv" ) x = df.drop("Sales" , axis=1 ) y = df["Sales" ]
1 2 3 4 5 count mean std min 25% 50% 75% max TV 200.0 147.0425 85.854236 0.7 74.375 149.75 218.825 296.4 Radio 200.0 23.2640 14.846809 0.0 9.975 22.90 36.525 49.6 Newspaper 200.0 30.5540 21.778621 0.3 12.750 25.75 45.100 114.0 Sales 200.0 14.0225 5.217457 1.6 10.375 12.90 17.400 27.0
1 2 3 4 5 TV Radio Newspaper Sales TV 1.000000 0.054809 0.056648 0.782224 Radio 0.054809 1.000000 0.354104 0.576223 Newspaper 0.056648 0.354104 1.000000 0.228299 Sales 0.782224 0.576223 0.228299 1.000000
2.2. 数据预处理
数据的预处理包括:数据的采样、数据的清洗、特征选择、特征降维、特征编码、规范化、数据集拆分等过程。
1 2 3 [x_train, x_test, y_train, y_test ] = train_test_split(x, y, random_state=1 )
2.3. 模型训练与预测
1 2 lr = LinearRegression() lr.fit(x_train, y_train)
1 2 3 4 5 lr_infer = lr.predict(x_test) lr_truth = list (y_test) print ("Round\t Truth \t Infer" )for i in range (len (lr_infer)): print ("%2s\t %5.2f \t %8.5f" % (i+1 , lr_truth[i], lr_infer[i]))
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 Round Truth Infer 1 23.80 21.70910 2 16.60 16.41055 3 9.50 7.60955 4 14.80 17.80770 5 17.60 18.61464 6 25.50 23.83574 7 16.90 16.32489 8 12.90 13.43226 9 10.50 9.17173 10 17.10 17.33385 11 14.50 14.44479 12 11.30 9.83512 13 17.40 17.18798 14 16.70 16.73087 15 13.40 15.05529 16 15.90 15.61434 17 12.90 12.42542 18 12.80 17.17716 19 9.50 11.08828 20 18.40 18.00538 21 10.70 9.28439 22 12.50 12.98458 23 8.50 8.79951 24 11.50 10.42382 25 11.90 11.38465 26 14.90 14.98083 27 10.10 9.78853 28 18.90 19.39643 29 19.60 18.18100 30 15.90 17.12808 31 23.20 21.54670 32 11.90 14.69809 33 17.30 16.24641 34 11.70 12.32115 35 20.20 19.92423 36 15.50 15.32499 37 11.50 13.88727 38 11.00 10.03162 39 22.30 20.93106 40 7.60 7.44937 41 5.30 3.64696 42 8.70 7.22020 43 6.70 5.99628 44 19.00 18.43382 45 5.50 8.39408 46 14.60 14.08371 47 14.60 15.02196 48 21.50 20.35836 49 22.60 20.57036 50 19.70 19.60637
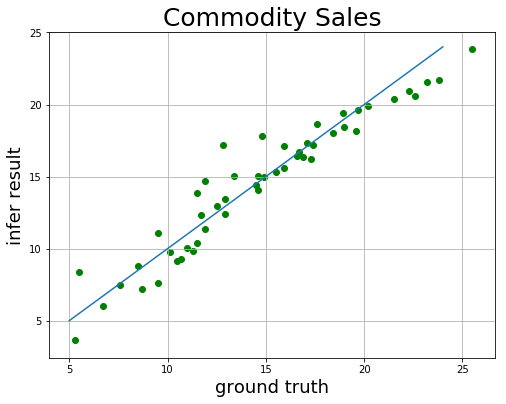
1 2 3 4 5 6 7 8 9 plt.figure(figsize=[8 , 6 ]) plt.title("Commodity Sales" , fontsize=25 ) x = np.arange(5 , 25 ) plt.plot(x, x) plt.xlabel("ground truth" , fontsize=18 ) plt.ylabel("infer result" , fontsize=18 ) plt.scatter(lr_truth, lr_infer, color="green" , label="sales" ) plt.grid() plt.show()
2.4. 模型评价
对于分类问题,评价测度是准确率,但这种方法不适用于回归问题,回归问题需要使用针对连续数值的评价测度。均方根误差,Root Mean Squared Error,RMSE )。
1 2 3 4 5 6 cols = ["TV" , "Radio" , "Newspaper" ] for i, val in enumerate (lr.coef_): print ("%s 的权重\t %.5f" % (cols[i], val)) print ("截距\t\t %.5f" % lr.intercept_)print ("训练集上的评分\t %.5f" % lr.score(x_train, y_train))print ("测试集上的评分\t %.5f" % lr.score(x_test, y_test))
1 2 3 4 5 6 TV 的权重 0.04656 Radio 的权重 0.17916 Newspaper 的权重 0.00345 截距 2.87697 训练集上的评分 0.89031 测试集上的评分 0.91562
1 2 3 4 mae_infer = metrics.mean_absolute_error(y_test, lr_infer) mse_infer = metrics.mean_squared_error(y_test, lr_infer) rmse_infer = np.sqrt(mse_infer) print ("MAE:%.6f \t MSE:%.6f \t RMSE:%.6f" % (mae_infer, mse_infer, rmse_infer))
1 MAE:1.066892 MSE:1.973046 RMSE:1.404651
2.5. 模型优化
由于Newspaper和销量之间的相关性非常小 (约0.00345),因此我们可以移除这个特征,然后看看线性回归模型预测结果的RMSE如何。
1 2 3 4 5 x = df[["TV" , "Radio" ]] y = df["Sales" ] [x_train, x_test, y_train, y_test ] = train_test_split(x, y, random_state=1 )
1 2 3 4 nlr = LinearRegression() nlr.fit(x_train, y_train) nlr_infer = nlr.predict(x_test) nlr_truth = list (y_test)
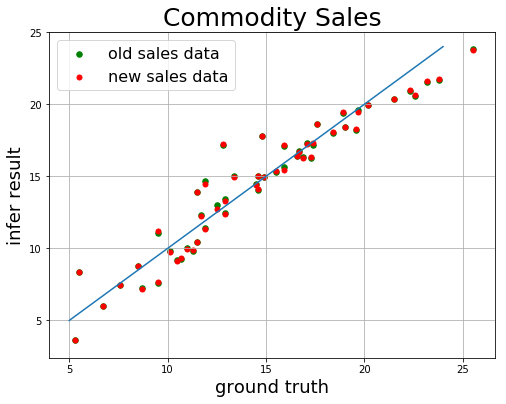
1 2 3 4 5 6 7 8 9 10 11 plt.figure(figsize=[8 , 6 ]) plt.title("Commodity Sales" , fontsize=25 ) x = np.arange(5 , 25 ) plt.plot(x, x) plt.xlabel("ground truth" , fontsize=18 ) plt.ylabel("infer result" , fontsize=18 ) plt.scatter(lr_truth, lr_infer, 30 , color="green" , label="old sales data" ) plt.scatter(nlr_truth, nlr_infer, 25 , color="red" , label="new sales data" ) plt.legend(loc="upper left" , fontsize=16 ) plt.grid() plt.show()
1 2 3 4 5 6 7 8 9 10 vals = list (nlr.coef_) print ("TV列的权重\t %.5f" % vals[0 ])print ("Radio列的权重\t %.5f" % vals[1 ])print ("截距\t\t %.5f" % nlr.intercept_)print ("训练集上的评分\t %.5f" % nlr.score(x_train, y_train))print ("测试集上的评分\t %.5f" % nlr.score(x_test, y_test))mse_infer = metrics.mean_squared_error(y_test, nlr_infer) rmse_infer = np.sqrt(mse_infer) print ("评价测度(RMSE)\t %.6f" % rmse_infer)
1 2 3 4 5 6 TV列的权重 0.04660 Radio列的权重 0.18118 截距 2.92724 训练集上的评分 0.89015 测试集上的评分 0.91762 评价测度(RMSE) 1.387903
3. 优化结论
由上面的结果可以看出,移除相关性较弱的特征后,均方根误差RMES会变得更小一点,模型的拟合效果也会更好。
机器学习中有“奥卡姆剃刀”的原理,如果能够用简单模型解决问题,那么就不使用复杂模型,因为复杂模型往往增加了不确定性,造成过多的人力和物力成本,且容易过拟合。
写在最后